La problématique
En 2000, les méthodes de conception des films en image de synthèse présentaient un certain paradoxe car elles font intervenir des outils aux bases mathématiques complexes (projection perspectives, courbes 3D d’interpolation, modèles complexes de caméra, modélisation des mouvements) et devraient pourtant pouvoir être utilisées par non–spécialistes (les artistes). L’approche que nous proposons, dirigée par les contraintes, est à l’opposé des méthodes actuelles qui forcent l’utilisateur à construire pas à pas le mouvement de caméra. De plus, il semble naturel que l’évolution des modeleurs s’accompagne de la prise en compte d’une part de plus en plus importante des mécanismes de base associés à la conception cinématographique (notions de panoramique, travelling, règles de composition, etc.).
La faisabilité
Ces notions sont modélisables de manière naturelle sous forme de systèmes de contraintes. Les principaux problèmes liés à la résolution de contraintes pour le calcul des solutions représentant les mouvements de caméra concernent la difficulté inhérente au type de contraintes à résoudre (non–linéarité, domaines continus, fonctions trigonométriques, espace de recherche de dimension élevée), la dimension temporelle (introduction de contraintes universellement quantifiées) et la sélection d’un sous-ensemble pertinent de solutions représentatives. Une approche statique par arithmétique d’intervalles et évaluation-subdivision
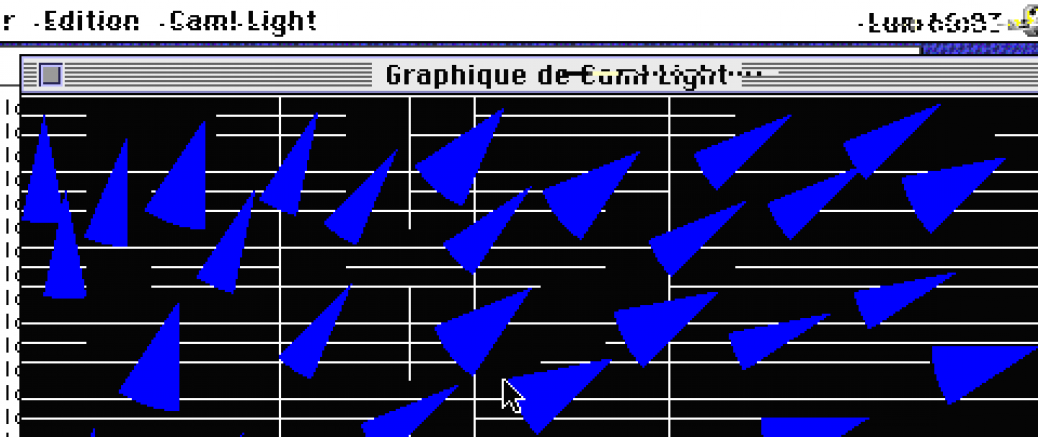
Une première approche de placement de vue en statique (objet et caméra statiques) a permis relativement rapidement de démontrer la faisabilité du solveur. Les formules de projections perspectives sont transformées en utilisant les fonctions d’intervalles (voir Moore). L’espace de recherche (position 3D et orientation 3D) est ensuite evalué, la fonction de projection (étendue aux intervalles) est appliquée donnant une réponse dans un domaine trivalué : vrai, faux, vrai-faux. Dans le dernier cas, on subdivise l’espace, on évalue et on recommence récursivement. On obtient une approximation intérieure de l’ensemble solution, qui peut ensuite être exploré.
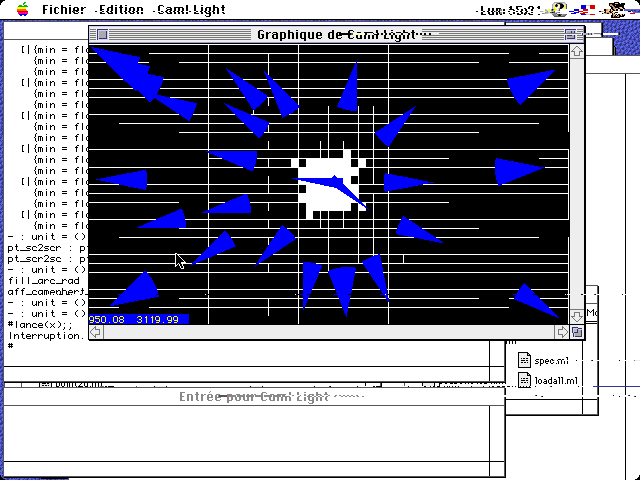
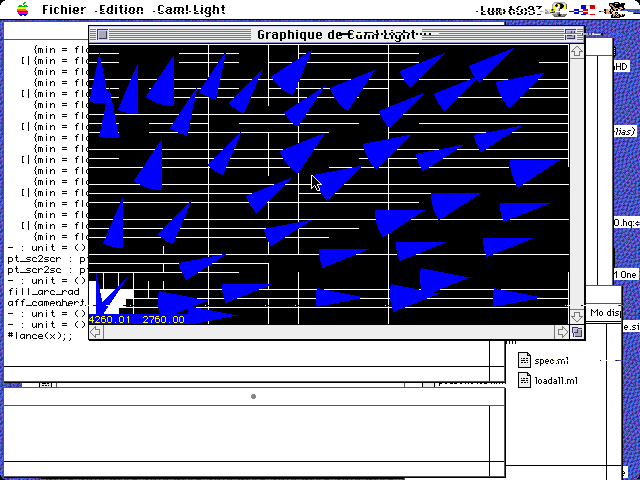
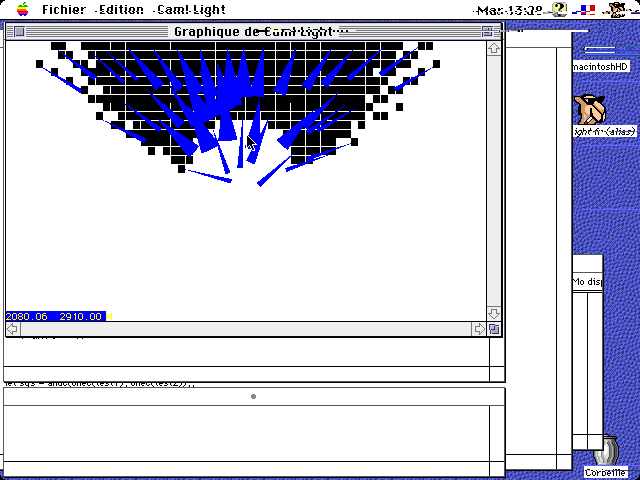
Les exemples montrent les hyper-pavés qui portent des solutions, les camemberts indiquant l’amplitude d’angle de caméra.
Une approche dynamique et le quantifieur universel
Pendant le stage de DEA de F.Jardillier, une approche dynamique a été développé. Cette version prenait en compte l’opérateur universellement quantifié qui est indispensable pour traiter les contraintes comme "l’objet A apparait dans la fenêtre pendant les 3 premières secondes". La prise en compte des objets mobiles et de la caméra mobile. L’évaluation-subdivision est ainsi appliquée sur une nouvelle dimension : le temps.
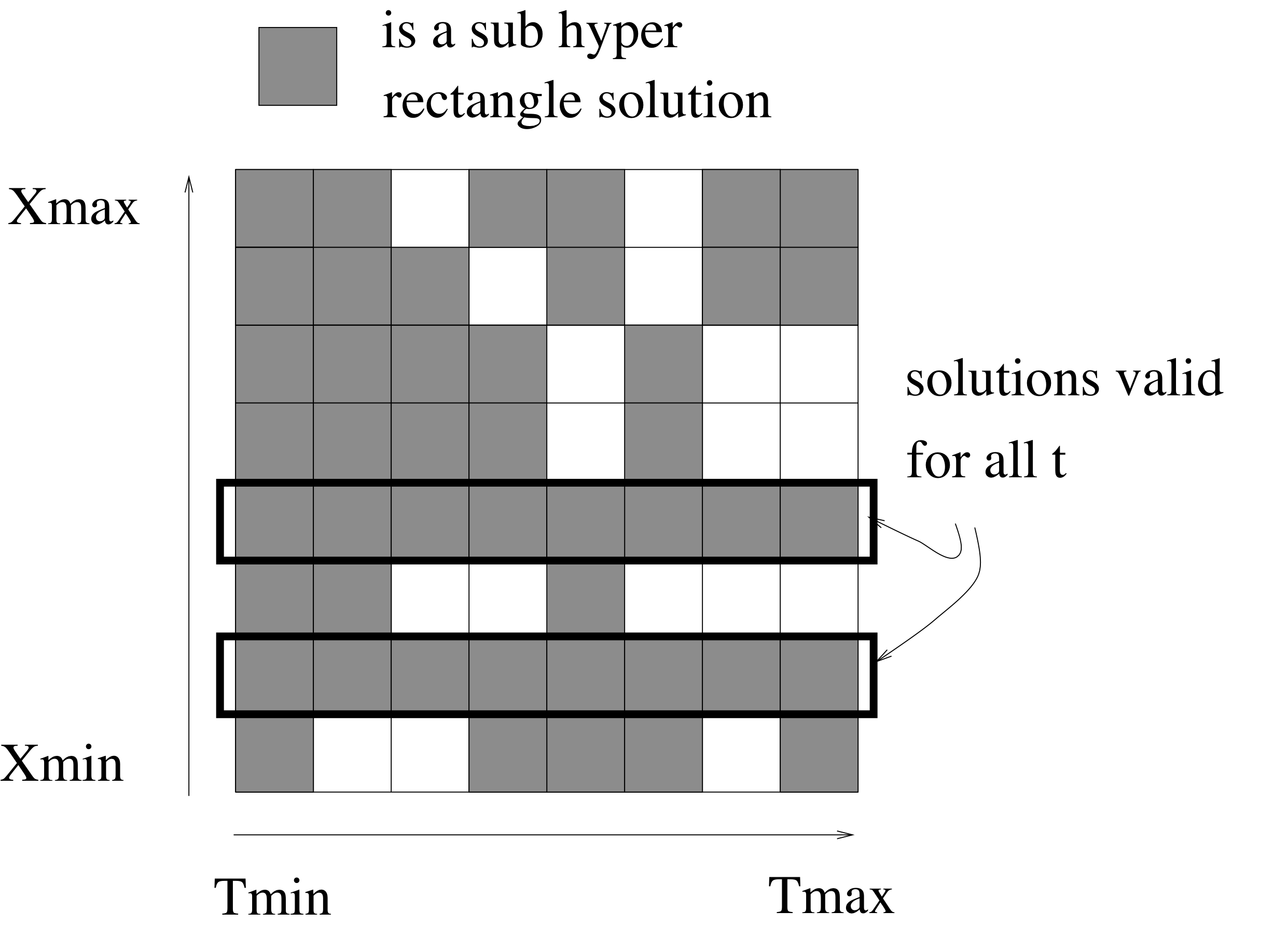
Quelque soit t
Un langage de spécification des contraintes cinématographiques est développé. La modélisation des mouvements de caméra utilise des splines, ce qui permet une caractérisation de l’espace de recherche.