1er juin 2022. Je viens de publier sur HAL un rapport de recherche, en anglais,
Titre : "Importance Driven Color Assignment"
Sous-titre : "Importance Driven Color-Group Assignment in Categorical Visualization"
sur mes derniers travaux à propos de l'affectation des couleurs à des classes dans le cadre de visualisations de données catégorielles.
Le fichier pdf est téléchargeable (utilisez sauver sous) ici
Dans les visualisations de données catégorielles, les différentes valeurs sont en général identifiées par des couleurs différentes. Chercher à la fois les couleurs à utiliser et à quelles valeurs les associer est compliqué, mais des publications existent sur cette question.
Je pense que les "data scientists" ont des préférences sur les palettes de couleurs à utiliser pour les visualisations de données catégorielles. C'est pour cette raison et parce que ça réduit l'espace de recherche, que le travail présenté dans ce rapport utilise une palette de couleurs fournie par l'utilisateur. Si il y a n catégories, l'utilisateur founit la palette contenant n couleurs. Il ne "reste" alors qu'à trouver à quelle catégorie associer chaque couleur.
Le problème reste compliqué (NP-complet), pour n couleurs il y a factorielle n possibilités d'affectation.
n! = 1x2x3x4x...x(n-2)x(n-1)x(n)
Il s'agit donc de permutations. Par exemple, pour 3 couleurs, il y a 1x2x3=6 façons de les affecter à des valeurs : (1,2,3)(1,3,2)(2,1,3)(2,3,1)(3,1,2)(3,2,1)
Pour trouver une solution (donc une permutation), passées les valeurs petites telles que n<8, il est trop long d'essayer toutes les permutations (pour 10 catégories, le nombre de permutations est de 3 628 800). Il faut donc essayer de trouver une solution satisfaisante par des méthodes heuristiques.
Pour modéliser le problème, on décide d'une fonction d'énergie (fitness) qui prend en entrée des paramètres à tester, et donc pour ce problème, une permutation, et cette fonction d'énergie doit rendre une valeur d'autant plus grande que la solution décrite par les paramètres (la permutation) est satisfaisante.
Pour élaborer cette fonction, j'utilise deux matrices carrées symétriques.
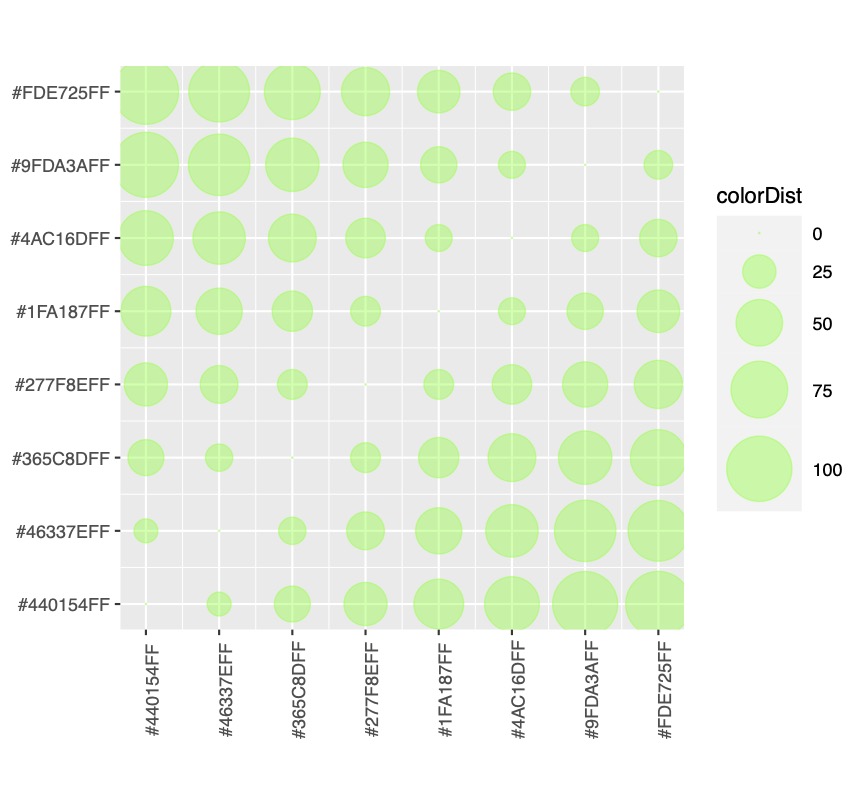
Matrice de distance de couleurs
La première est une matrice de distance de couleurs (indépendante des données), qui contient les n x n distances entre les couleurs de la palette (J'utilise la disatnce DE2000 élaborée par la CIE).
L'élément i,j de la matrice de couleur contient donc résultat de la distance de couleur DE2000 entre les deux couleurs Ci et Cj de la palette. Cette valeur est indépendante des données et indépendante du type de visualisation.
Matrice d'importance
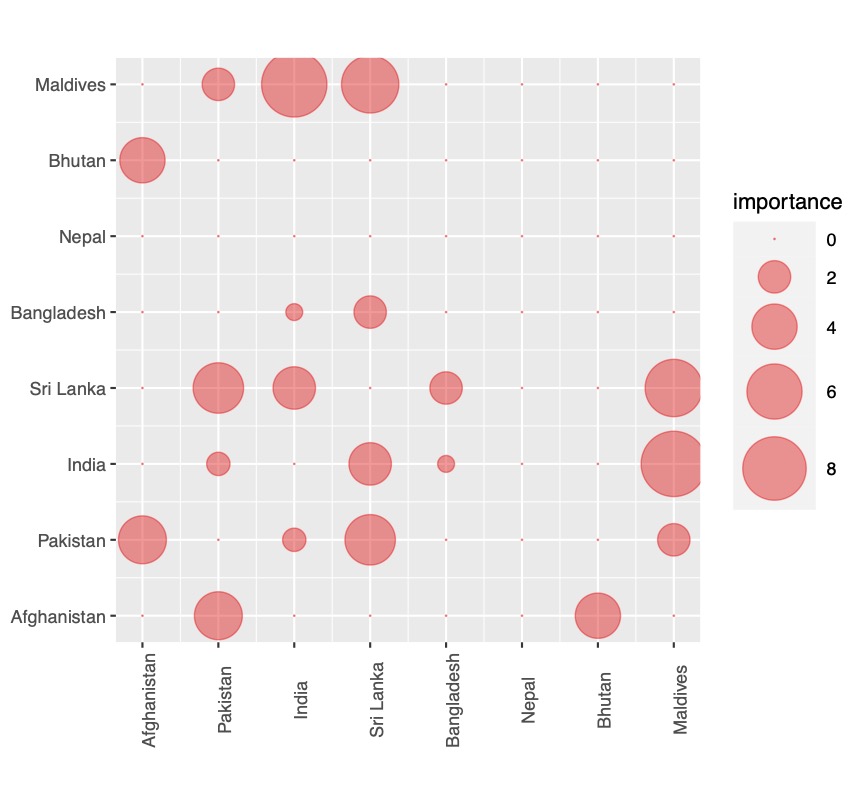
La seconde matrice (de taille n x n ) dite "d'importance" (indépendante des couleurs) code l'importance d'avoir un contraste de couleurs élevé entre deux classes de la visualisation (entre deux objets graphiques, ou deux ensembles d'objets graphiques représentant des classes).
L'élément i,j de la matrice d'importance contient le besoin de contraste de couleurs entre les deux objets de la visualisation qui représentent les catégories i et j. La valeur de cet élément est indépendante des couleurs mais dépendante du type de visualisation et des données représentées. Par exemple, si deux objets graphiques sont voisins et de petites tailles le besoin de contraste sera élévé afin de ne pas les confondre si des couleurs proches leurs sont affectées.
Estimation de la réussite d'une affectation
Nous considérons que la réussite d'une affectation de couleur p à une classe q est alors modélisée par le produit des deux élément p,q des deux matrices. Pour tenir compte de la permuation évaluée, il faut changer l'ordre des couleurs et donc permuter la matrice de couleurs.
La réussite d'une permutation peut être modélisée par la somme des réussites individuelles. Par conséquent, l'énergie pour une permutation, est égale à la somme des produits des éléments des deux matrices, terme à terme. Ce produit (non conventionnel) de matrices est appelé produit de Frobenius.
Optimisation
Un algorithme d'optimisation génétique (paramétré pour coder des permutations) fournit une solution approchée (une permutation) pour laquelle l'énergie calculée est la plus haute.
Application
Pour appliquer le concept, il est alors nécessaire de formuler ,pour chaque type de visualisation, une expression mathématique calculant le besoin de contraste entre deux classes d'objets graphiques.
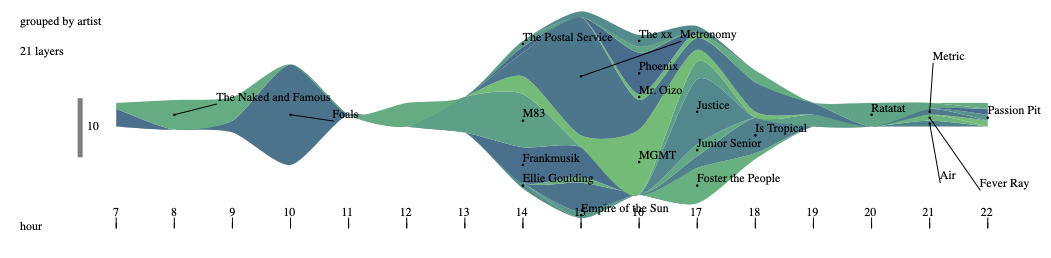
Les formules pour plusieurs types de visualisation sont explicitées dans le rapport, streamgraph, chord diagram, line charts, carte polygonale. Les résultats d'affectation sont comparées avec des affectations aléatoires de couleurs et des affectation conservant l'ordre des couleurs de la palette.
En cliquant sur les images, l'image en pdf est accessible.
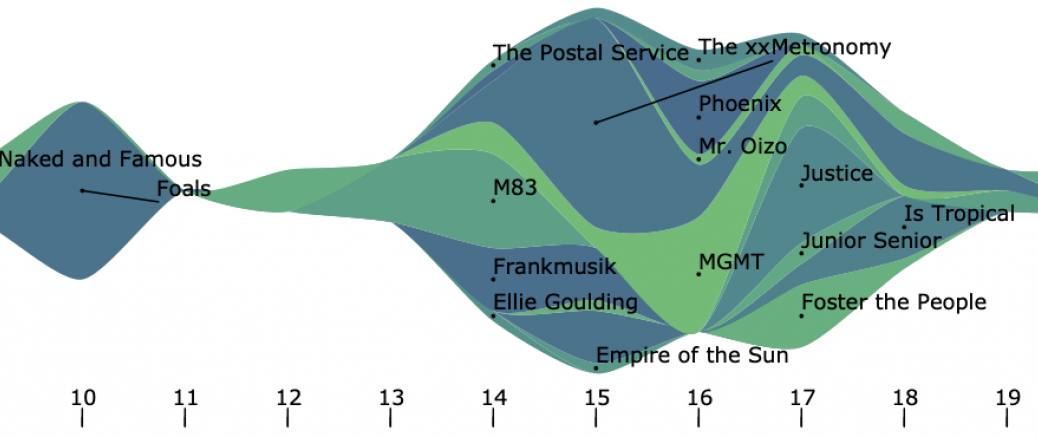
Visualisation en "Streamgraph", sur des donnés d'écoutes musicales (projet Musimorphose)
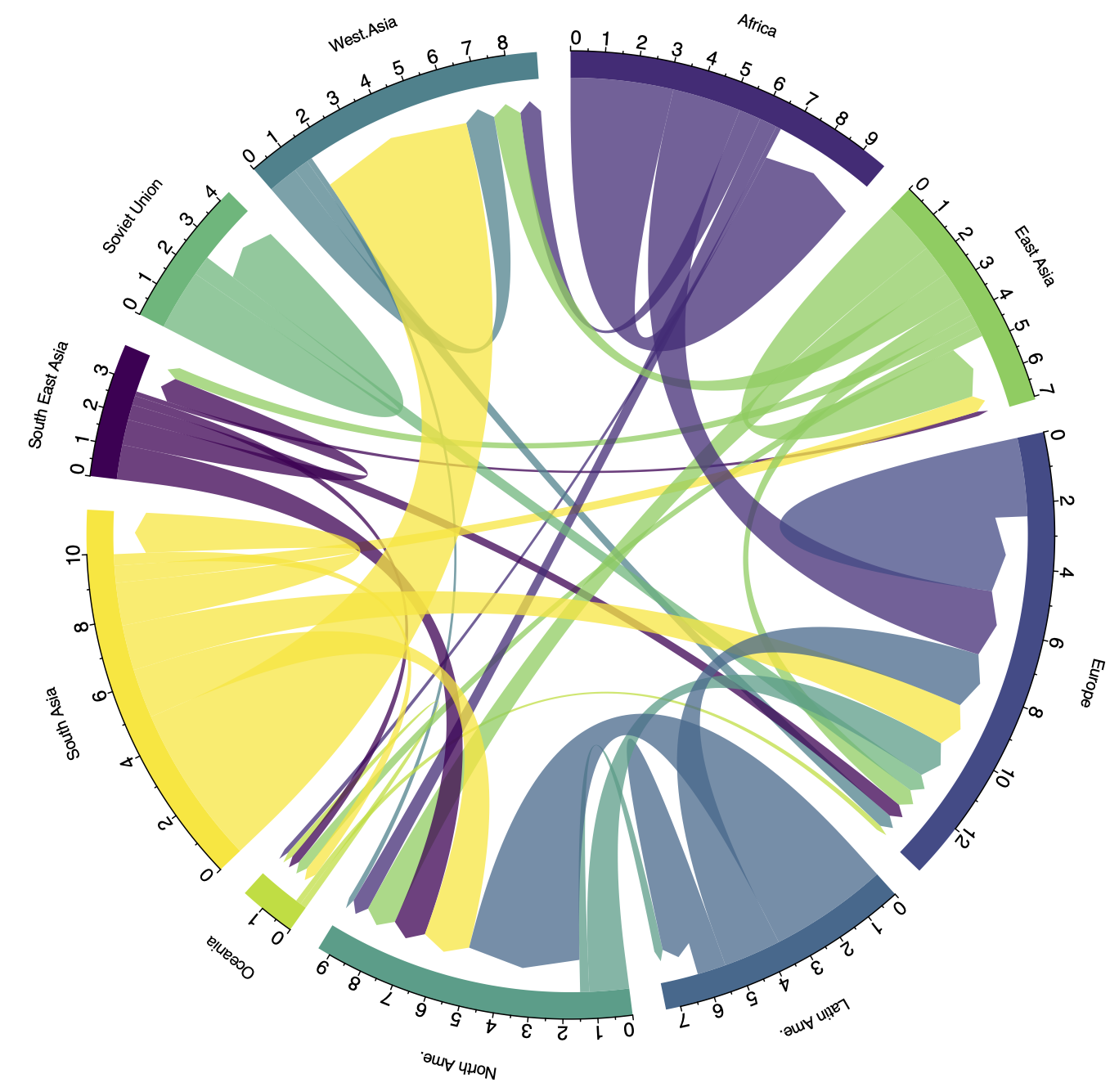
Visualisation en "Chord diagram", d'après www.data-to-viz.com (merci à Yan Holtz), avec notre affectation de couleurs optimisée
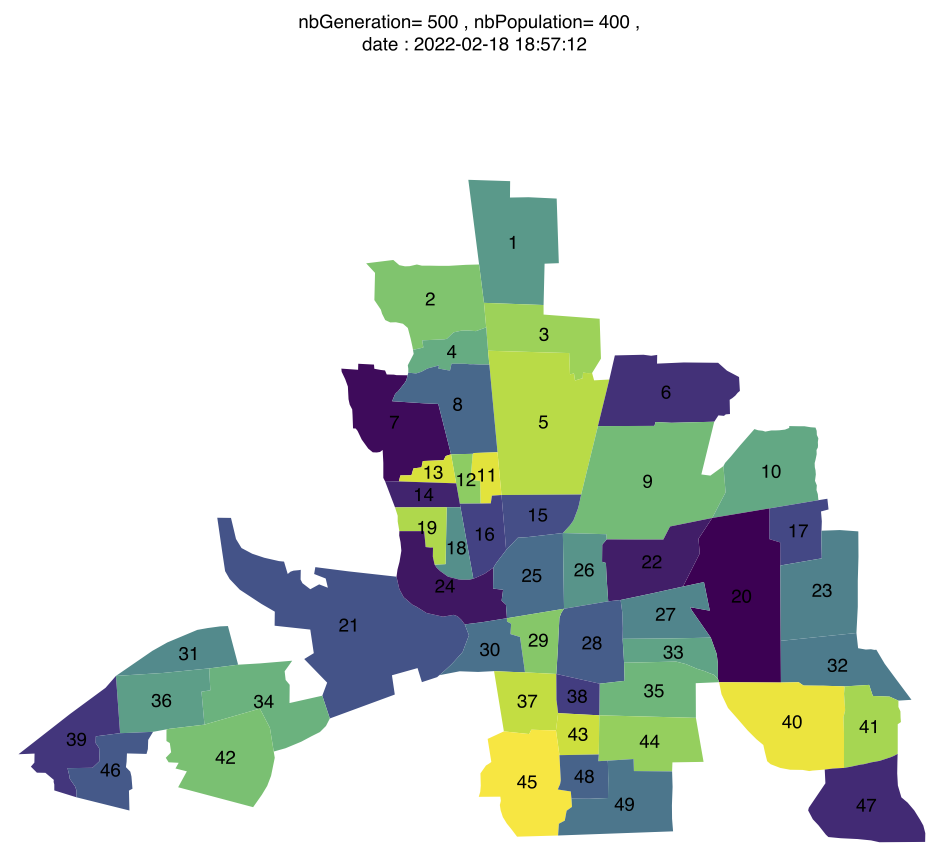
Visualisation de catégories en carte polygonale ( package R spdep ).
Colombus map